The eta parameter in XGBoost, also known as the learning rate, controls the step size at each boosting iteration.
It is a crucial hyperparameter that influences the model’s convergence speed and performance.
An alias for the eta parameter is learning_rate.
Smaller values of eta lead to slower convergence but can result in better generalization, while larger values may cause the model to converge faster but might lead to suboptimal solutions.
This example demonstrates how to tune the eta hyperparameter using grid search with cross-validation to find the optimal value that balances convergence speed and model performance.
import xgboost as xgb
import numpy as np
from sklearn.datasets import make_regression
from sklearn.model_selection import GridSearchCV, KFold
from sklearn.metrics import mean_squared_error
# Create a synthetic dataset
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=42)
# Configure cross-validation
cv = KFold(n_splits=5, shuffle=True, random_state=42)
# Define hyperparameter grid
param_grid = {
'eta': [0.01, 0.05, 0.1, 0.2, 0.3]
}
# Set up XGBoost regressor
model = xgb.XGBRegressor(n_estimators=100, objective='reg:squarederror', random_state=42)
# Perform grid search
grid_search = GridSearchCV(estimator=model, param_grid=param_grid, cv=cv, scoring='neg_mean_squared_error', n_jobs=-1, verbose=1)
grid_search.fit(X, y)
# Get results
print(f"Best eta: {grid_search.best_params_['eta']}")
print(f"Best CV MSE: {-grid_search.best_score_:.4f}")
# Plot eta vs. MSE
import matplotlib.pyplot as plt
results = grid_search.cv_results_
plt.figure(figsize=(10, 6))
plt.plot(param_grid['eta'], -results['mean_test_score'], marker='o', linestyle='-', color='b')
plt.fill_between(param_grid['eta'], -results['mean_test_score'] + results['std_test_score'],
-results['mean_test_score'] - results['std_test_score'], alpha=0.1, color='b')
plt.title('Learning Rate (eta) vs. MSE')
plt.xlabel('Learning Rate (eta)')
plt.ylabel('CV Average MSE')
plt.grid(True)
plt.show()
The resulting plot may look as follows:
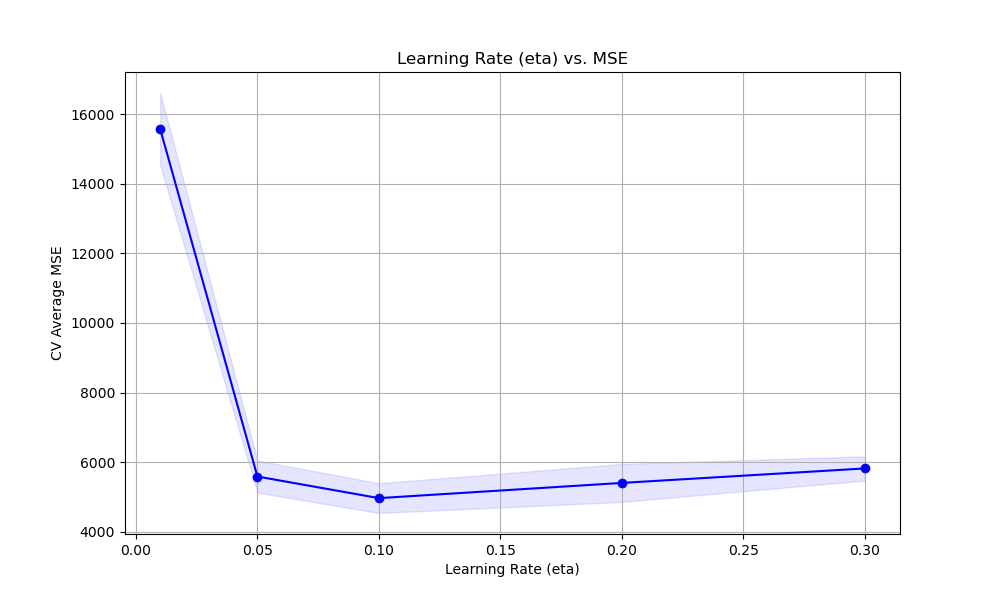
In this example, we create a synthetic regression dataset using scikit-learn’s make_regression function. We then set up a KFold cross-validation object to split the data into training and validation sets.
We define a hyperparameter grid param_grid that specifies the range of eta values we want to test. In this case, we consider values [0.01, 0.05, 0.1, 0.2, 0.3].
We create an instance of the XGBRegressor with some basic hyperparameters set, such as n_estimators and objective. We then perform the grid search using GridSearchCV, providing the model, parameter grid, cross-validation object, scoring metric (negative mean squared error), and the number of CPU cores to use for parallel computation.
After fitting the grid search object with grid_search.fit(X, y), we can access the best eta value and the corresponding best cross-validation mean squared error (MSE) using grid_search.best_params_ and grid_search.best_score_, respectively.
Finally, we plot the relationship between the eta values and the cross-validation average MSE scores using matplotlib. We retrieve the results from grid_search.cv_results_ and plot the mean MSE scores along with the standard deviation as error bars. This visualization helps us understand how the choice of eta affects the model’s performance and guides us in selecting an appropriate value.
By tuning the eta hyperparameter using grid search with cross-validation, we can find the optimal learning rate that balances the model’s convergence speed and performance. This helps ensure that the model converges to a good solution while avoiding suboptimal results.
