The reg_alpha parameter in XGBoost controls the L1 regularization term, which adds a penalty proportional to the absolute value of the coefficients.
Tuning reg_alpha can help prevent overfitting by shrinking the coefficients of less important features, leading to a simpler and more generalizable model.
This example demonstrates how to tune the reg_alpha hyperparameter using grid search with cross-validation to find the optimal value that balances regularization and model performance.
import xgboost as xgb
import numpy as np
from sklearn.datasets import make_regression
from sklearn.model_selection import GridSearchCV, KFold
from sklearn.metrics import mean_squared_error
# Create a synthetic dataset
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=42)
# Configure cross-validation
cv = KFold(n_splits=5, shuffle=True, random_state=42)
# Define hyperparameter grid
param_grid = {
'reg_alpha': [0, 0.1, 0.5, 1, 5, 10]
}
# Set up XGBoost regressor
model = xgb.XGBRegressor(n_estimators=100, learning_rate=0.1, random_state=42)
# Perform grid search
grid_search = GridSearchCV(estimator=model, param_grid=param_grid, cv=cv, scoring='neg_mean_squared_error', n_jobs=-1, verbose=1)
grid_search.fit(X, y)
# Get results
print(f"Best reg_alpha: {grid_search.best_params_['reg_alpha']}")
print(f"Best CV MSE: {-grid_search.best_score_:.4f}")
# Plot reg_alpha vs. MSE
import matplotlib.pyplot as plt
results = grid_search.cv_results_
plt.figure(figsize=(10, 6))
plt.plot(param_grid['reg_alpha'], -results['mean_test_score'], marker='o', linestyle='-', color='b')
plt.fill_between(param_grid['reg_alpha'], -results['mean_test_score'] + results['std_test_score'],
-results['mean_test_score'] - results['std_test_score'], alpha=0.1, color='b')
plt.title('Reg Alpha vs. MSE')
plt.xlabel('Reg Alpha')
plt.ylabel('CV Average MSE')
plt.grid(True)
plt.show()
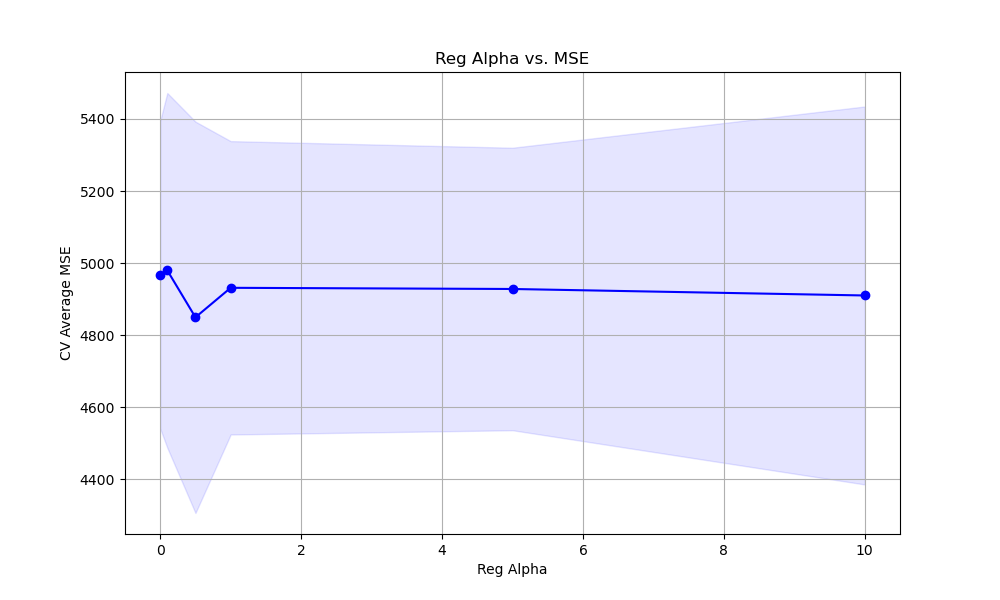
The resulting plot may look as follows:
In this example, we create a synthetic regression dataset using scikit-learn’s make_regression function. We then set up a KFold cross-validation object for splitting the data into training and validation sets.
We define a hyperparameter grid param_grid that specifies the range of reg_alpha values we want to test, including 0 (no regularization) and several positive values.
We create an instance of the XGBRegressor with basic hyperparameters set, such as n_estimators and learning_rate. We then perform the grid search using GridSearchCV, providing the model, parameter grid, cross-validation object, scoring metric (negative mean squared error), and the number of CPU cores to use for parallel computation.
After fitting the grid search object with grid_search.fit(X, y), we can access the best reg_alpha value and the corresponding best cross-validation mean squared error using grid_search.best_params_ and grid_search.best_score_, respectively.
Finally, we plot the relationship between the reg_alpha values and the cross-validation average mean squared error scores using matplotlib. We retrieve the results from grid_search.cv_results_ and plot the mean MSE scores along with the standard deviation as error bars. This visualization helps us understand how the choice of reg_alpha affects the model’s performance and guides us in selecting an appropriate value.
By tuning the reg_alpha hyperparameter using grid search with cross-validation, we can find the optimal level of L1 regularization that minimizes overfitting and improves the model’s generalization performance.
