The min_split_loss parameter in XGBoost is a regularization hyperparameter that controls the minimum loss reduction required to make a further partition on a leaf node of the tree.
An alias for the min_split_loss parameter is gamma.
It can be used to control the complexity of the model and help prevent overfitting. Higher values of min_split_loss make the model more conservative and can lead to underfitting, while lower values allow the model to make more splits and capture more details in the data, potentially leading to overfitting.
This example demonstrates how to tune the min_split_loss hyperparameter using grid search with cross-validation to find the optimal value that balances model complexity and performance.
import xgboost as xgb
import numpy as np
from sklearn.datasets import make_regression
from sklearn.model_selection import GridSearchCV, KFold
from sklearn.metrics import mean_squared_error
# Create a synthetic dataset
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=42)
# Configure cross-validation
cv = KFold(n_splits=5, shuffle=True, random_state=42)
# Define hyperparameter grid
param_grid = {
'min_split_loss': [0, 0.1, 0.2, 0.5, 1, 2, 5]
}
# Set up XGBoost regressor
model = xgb.XGBRegressor(n_estimators=100, learning_rate=0.1, random_state=42)
# Perform grid search
grid_search = GridSearchCV(estimator=model, param_grid=param_grid, cv=cv, scoring='neg_mean_squared_error', n_jobs=-1, verbose=1)
grid_search.fit(X, y)
# Get results
print(f"Best min_split_loss: {grid_search.best_params_['min_split_loss']}")
print(f"Best CV MSE: {-grid_search.best_score_:.4f}")
# Plot min_split_loss vs. MSE
import matplotlib.pyplot as plt
results = grid_search.cv_results_
plt.figure(figsize=(10, 6))
plt.plot(param_grid['min_split_loss'], -results['mean_test_score'], marker='o', linestyle='-', color='b')
plt.fill_between(param_grid['min_split_loss'], -results['mean_test_score'] + results['std_test_score'],
-results['mean_test_score'] - results['std_test_score'], alpha=0.1, color='b')
plt.title('Min Split Loss vs. MSE')
plt.xlabel('Min Split Loss')
plt.ylabel('CV Average MSE')
plt.grid(True)
plt.show()
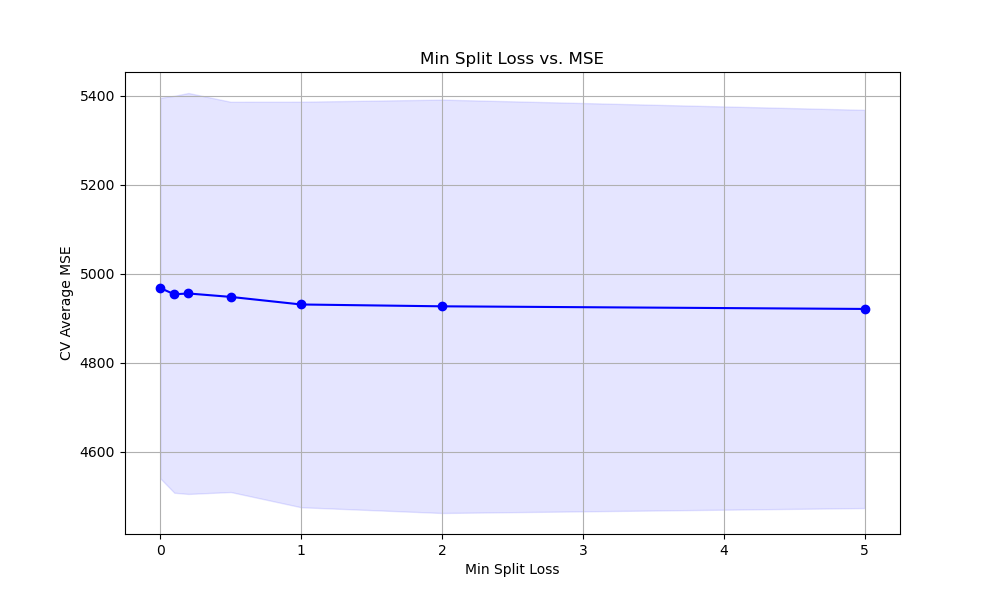
The resulting plot may look as follows:
In this example, we create a synthetic regression dataset using scikit-learn’s make_regression function. We then set up a KFold cross-validation object to split the data into training and validation sets.
We define a hyperparameter grid param_grid that specifies the range of min_split_loss values we want to test. The values chosen here are for demonstration purposes and may need to be adjusted based on the specific dataset and problem.
We create an instance of the XGBRegressor with some basic hyperparameters set, such as n_estimators and learning_rate. We then perform the grid search using GridSearchCV, providing the model, parameter grid, cross-validation object, scoring metric (negative mean squared error), and the number of CPU cores to use for parallel computation.
After fitting the grid search object with grid_search.fit(X, y), we can access the best min_split_loss value and the corresponding best cross-validation mean squared error using grid_search.best_params_ and grid_search.best_score_, respectively.
Finally, we plot the relationship between the min_split_loss values and the cross-validation average mean squared error scores using matplotlib. We retrieve the results from grid_search.cv_results_ and plot the mean MSE scores along with the standard deviation as error bars. This visualization helps us understand how the choice of min_split_loss affects the model’s performance and guides us in selecting an appropriate value.
By tuning the min_split_loss hyperparameter using grid search with cross-validation, we can find the optimal value that balances the model’s complexity and performance. This helps prevent overfitting and ensures that the model generalizes well to unseen data.
